Adding a Dimension
Derivation of matrix form of rotation around z axis and projection using similar triangles (codes at the bottom if you want to skip the derivation).
Matrix rotation
Point P can be defined with coordinates u,v it can also be defined by polar coordinates
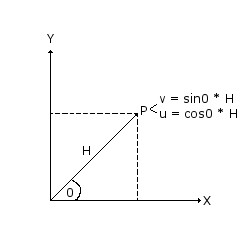
Rotation P around a fixed point (Z) can be defined as follows
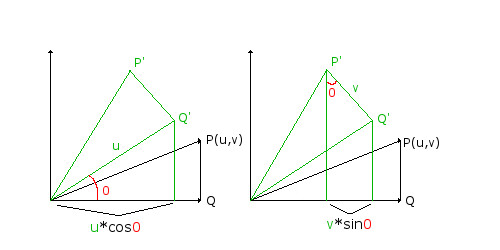
Since the shape and size of the right angle triangle is unchanged by the rotation around angle 0, it follows that side Q' has length u and side Q'P' has length v. Thus the x coordinate of P' after rotation through 0 can be written as
P'(u) = u*cos0 - v*sin0
and the y coordinate of P' after rotation through 0 can be written as
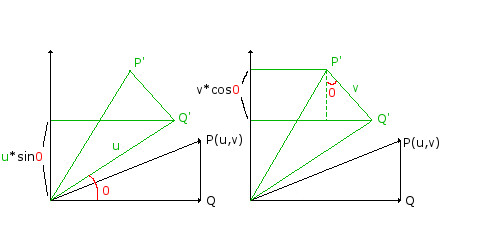
P'(v) = u*sin0 + v*cos0
which together can be written as
P(u,v) = (u*cos0 - v*sin0, u*sin0 + v*cos0)
In vector form P(u,v) under the rotation 0 can be written as

which can be written as the matrix product
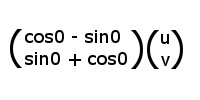
As we are rotating around z (which will be unchanged by the rotation) the final matrix product will be

Replace u with x, and v with y and the have the same rotation matrix in chapter50 (keep scrolling if you want the code).
Projection using similar triangles
Projection of 3D point in view space to screen space can be done using a simile triangles derived equation. The diagram below shows a point P in 3D space and point P' showing it projected onto screen space.
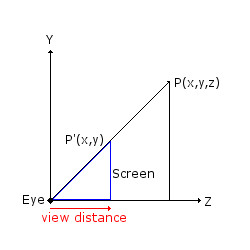
As P' forms a similar triangle (in blue) with that of P (in black) the following is true
P'(x) / view distance = P(x) / P(z)
P'(x) = (P(x)/P(x)) * view distance.
In this chapter of the book view distance is defined as -2 (#define PROJECTION_RATIO -2) and the result is scaled by the screen width / 2. Therefore the projection equation becomes
P'(x) = ((P(x)/P(x)) * PROJECTION_RATIO) * SCREEN_WIDTH / 2
Finally here is the code for chapter50